為替レートの値動きの従う確率分布

為替レートの値幅の定義

ある一定期間の為替レートの変動を考えたとき，その期間における「終値と始値の差」を値動きと呼ぶことにしよう．

\[ \text{値動き} \, (\text{difference}) = \text{終値} \, (\text{close}) \, – \, \text{始値} \, (\text{open}) \ . \]

（「値動き」という単語はちょっと格好が悪いが，こなれた日本語を思いつかないので仕方がない．ちなみに「値幅」は「高値と安値の差」という意味で使うことにしている）

ある期間で値上がりをした場合には値動きは正，値下がりをした場合には値動きは負となる．もし値上がりと値下がりが同程度の大きさと頻度で起こるならば，値動きの分布は平均値（中央値と言ってもよい）がゼロの左右対称な分布になることが期待される．

このページでは，為替レートの値動きがどのような分布をしているのか，ドル円の日足データを例として確かめてみる．

ドル円の日足データの値幅分布

ドル円の日足データには，ある証券会社の2007年1月から2019年12月までの13年間（計3,371営業日）のヒストリカルデータを用いた．これらのデータから値動きのヒストグラムを作ると，下図のようになる．

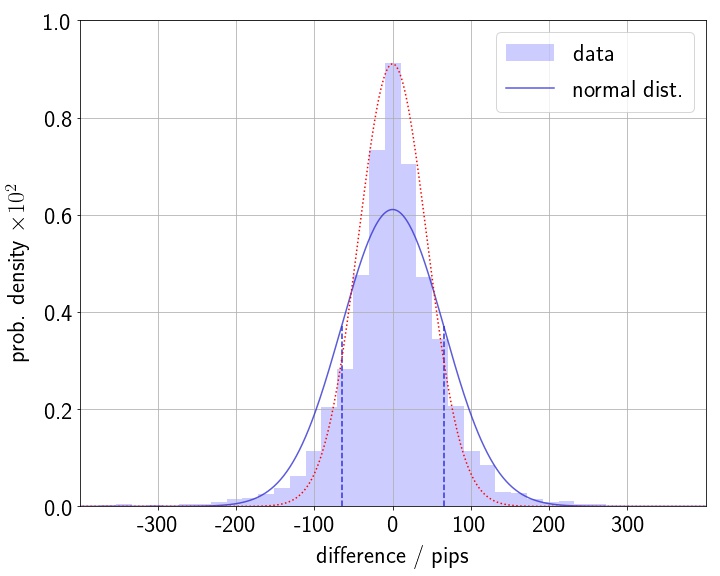
図の横軸はpipsを単位とした値動き，縦軸は規格化した度数（確率密度）である．図を見ると確かにゼロを中心とした左右対称の分布になっていることがわかる．つまり，値上がりと値下がりが同程度の大きさと頻度で起こっていると言って良い．

一見すると，この分布は正規分布のように見える．しかし，データから計算される中央値$m = 0$と標準偏差$\sigma = 65.317 \, \text{pips}$を持つ正規分布（図の青の実線）では，このデータの分布をうまくフィットすることができない．

標準偏差をもう少し小さくして，幅の狭い正規分布のほうがフィットが良くなりそうな気もするが，図中の赤い点線で示したように，この場合には裾野の広がりがうまく説明できない．したがって，為替データの値動きの分布は正規分布には従わないということを意味している．

値動きの従う分布は，定性的には正規分布よりも中央に寄った尖度の高い分布になっている．この傾向は時間足や週足などの異なる時間スケールの値動きの分布についても変わらない．（為替レートのスケール不変性）

また，値動きそのものではなく，値動きをその時の為替レートで割った「値動き率」の分布を考えても同様である．

値動き分布が正規分布に従わないことについて

為替レートの1日の動きは1時間の動きから，1時間の動きは1分の動きから作られる．一般に，ある期間の為替レートの動きは，それよりも短い期間の動きの累積として得られる．

たとえば，日足データは1,440個の1分足データから作られる．もし為替レートが完全なランダムウォークならば，1分足の値動きの分布がどのような分布に従おうとも，（分布が有限の期待値と分散を持つ限り）その累積として与えられる日足データの値動きは，中心極限定理 [Ref.] によって正規分布に従うはずである．（1440は中心極限定理を適用するのに十分な数だろう）

値動き分布が正規分布に従わないという事実には，少なくとも2つの原因が考えられる．ひとつは為替レートの値動きがランダムウォークではないという可能性，もうひとつは値動き分布が有限の期待値と分散を持たない可能性である．以下でそれぞれの可能性について簡単にコメントしておこう．（著者は現時点で答えを持っていない）

為替レートの値動きがランダムウォークではない可能性

為替レートが完全にはランダムウォークであるはずがないと信じる人は大勢いるだろう．FXトレーダーの大部分はそう考えているかもしれない．もし為替レートが本当にランダムウォークするのなら「トレンド」など幻想の産物で，あらゆるテクニカル分析が意味を為さなくなるのだから．

実際のところ，為替レートはほとんどランダムウォークだとは思っているが，少しくらいは予想できる部分があるはずだというのが，おおかたの感覚ではないだろうか．

ある現象が本当にランダムであると確かめるのは容易ではない．「ランダムではない」ことは反例を挙げて簡単に証明できるが，「ランダムである」ことを証明するのはまさに「悪魔の証明」で，ほとんど不可能である．

値動き分布が有限の期待値と分散を持たない可能性

普段から物理学や数学に接している立場から見れば，こちらの可能性の方が尤もらしく思われる．期待値や分散を持たない分布というのは別に奇妙なものではなく，物理学などでも実際の問題として現れる．

たとえば，共鳴現象などを記述する際に現れるCauchy分布 [Ref.] がある（Lorentz分布とも呼ばれる）．この分布は$f(x) \propto (1 + x^{2})^{-1}$という形をしており，裾野が$f(x) \sim x^{-2}$のように振舞うため$x^{n} \, (n \ge 1)$を掛けた積分は収束せず，平均値や分散を持たない（定義することができない）．

また，Cauchy分布は安定分布 [Ref.] であるという特徴を持つ．Cauchy分布に従う確率変数の和も再びCauchy分布に従うのである．このことは，どの時間スケールで見ても値動きの分布が同じ形の分布に従っている（ように見える）という事実と矛盾しない．

したがって，もし値動き分布がCauchy分布のように期待値や分散を持たず，また安定分布になっているならば，値動きについての全ての性質を矛盾なく説明することができる．

値動き分布がCauchy分布に従ってくれれば話は簡単なのであるが，残念ながらCauchy分布でもデータをうまくフィットすることができない．実用上は値動きが従う分布を具体的な関数で表すことは必須ではないが，関数形が分かっていれば様々な量を解析的に計算できて便利である．

値動き分布のフィット関数についての現象論的な提案

関数形の提案

値動き分布をある程度よくフィットでき，かつできるだけ簡単な形をしているものとして，以下のような関数を提案する．

\[ f(x) = \frac{A}{x^{2} + x_{0}^{2}} \cdot \exp \left( -\frac{x^{2}}{2\sigma^{2}} \right) \ . \]

$A$は確率の和（積分）が$1$となるように決める規格化定数で，今の場合には$A = A(x_{0}, \sigma^{2})$のように分布のパラメータ$x_{0}$と$\sigma^{2}$の関数である．この分布はCauchy分布と正規分布（Gauss分布）の積になっている．（簡単に調べた範囲では，この分布には名前は付いていないようである）値動きの分布はゼロが中心なので，期待値（あるいは中央値，最頻値）はゼロとした．

この分布には値動き$x$に関して2つのスケール$x_{0}$と$\sigma$が含まれている．あとで分かるように，フィット がうまくいくのは$x_{0} < \sigma$の場合である．つまり，値動き$x$が小さい時（$x < \sigma$）はCauchy分布に近く，ある程度大きくなると（$x \sim \sigma$）指数関数的な減衰が効いてくる．

この分布はCauchy分布にGauss関数型の収束因子を掛けたものと見ることができ，期待値や分散が有限の値として求まる．したがって，先に述べたような望ましい性質を備えているわけではない．しかしながら，$x < \sigma$の場合には分布はCauchy分布に近いため，この範囲ではそれらの性質を近似的に持っていると言ってよい．

この関数形は，様々な関数形の中からうまくいくものを探し出した現象論的なもので，背後にある為替レート変動の力学に依拠したものでは全く無いということに注意しておく．

データのフィット

データを関数でフィットする方法はたくさんあるが，ここでは簡単に，0次，2次，4次のモーメントを使ってパラメータ$(A, x_{0}, \sigma^{2})$を決めることにしよう．（偶関数なので，奇数次のモーメントはゼロ）

0次のモーメントは単なる確率の規格化である．また，値動きの期待値がゼロなので，2次のモーメントは分散に一致する．（細かいことを言えば，標本平均はゼロから少しずれるので，2次のモーメントは分散から少しずれる）3つのパラメータ$(A, x_{0}, \sigma^{2})$を決めるためには，これらに加えてもう一つ条件が必要なので，適当に4次のモーメントを選んだ．（ただし，高次のモーメントは外れ値に大きく影響を受けるので，詳細な解析には別の方法を用いるのが望ましいと思われる）

データからは，以下のような数値が得られる．

\begin{align*} \int_{-\infty}^{\infty}dx \, f(x) &= 1 \ , \\ \int_{-\infty}^{\infty}dx \, x^{2}f(x) &= 4.27 \times 10^{3} \ , \\ \int_{-\infty}^{\infty}dx \, x^{4}f(x) &= 1.73 \times 10^{8} \ , \\ \end{align*}

これらより$(A, x_{0}, \sigma^{2})$は，だいたい

\[ A = 15.17 \ , \quad x_{0} = 40 \ , \quad \sigma^{2} = 3 \times 10^{4} \quad (\sigma = 173) \ , \]

と求まる．フィッティング関数の形とフィッティングの手法が良くないので，あまり厳密に数字を合わせようとするとフィッティングはむしろ悪くなる．$(x_{0}, \sigma^{2})$を一桁かせいぜい二桁でおおらかに合わせるくらいでよい．規格化定数$A$は$(x_{0}, \sigma^{2})$を与えれば厳密に計算できる．このとき，2次と4次のモーメントはそれぞれ$5 \times 10^{3}$と$1.9 \times 10^{8}$となって，だいたい合っている．

先ほどと同様のヒストグラムをフィッティング関数と共に示す．

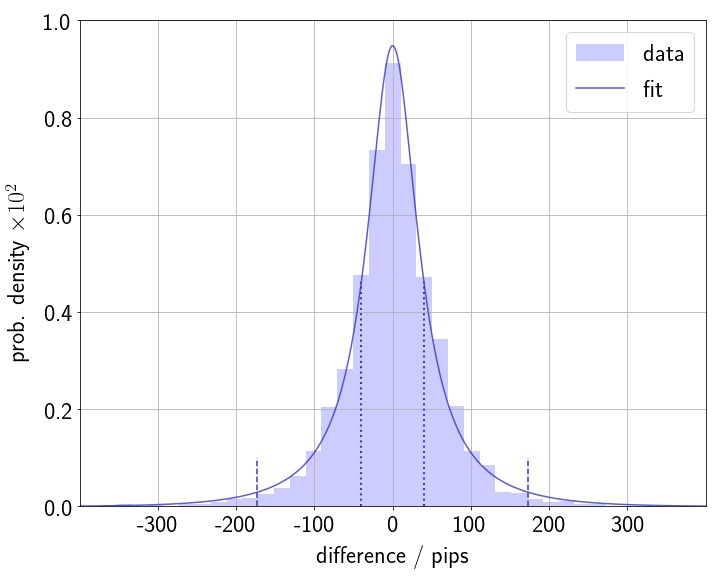
裾野の部分のフィット がやや甘いが，正規分布によるフィットと比べると遥かにうまくいっていることがわかる．ここでは示していないが，Cauchy分布によるフィットと比べても明らかに良い．

さしあたって値動き分布の解析的な表式が必要な場合はこのフィッティング関数を用いることにする．（値動きの理論に基づいた）より良いフィッティング関数が見つかれば，この部分は大幅に書き換える可能性がある．