最終更新日 : 2020/04/22
為替レートの値動き・値幅の自己相関
「為替レートの動きは予測できるのか?」というのは,トレーダーなら誰しも答えを知りたいと思っている問いである.このページでは,この問いに部分的にでも答えることを目的として,データ解析を行う.
いわゆるテクニカル分析に基づいたトレード手法というのは,そのほとんどが為替レートの動きが予測できるという仮定に基づいていると言って良い.ある手法では高値や安値の更新が続くトレンドの存在を仮定し,別の手法では相場が反転するパターンのようなものが存在すると主張する.
もしトレンドが存在するなら,ある期間に為替レートが上昇(下降)すると,その次の期間も上昇(下降)しやすいという傾向が見られるはずである.あるいは,上昇(下降)がある程度の期間続いた後に反発しやすいという傾向があるならば,その手がかりが為替レートのデータの中に含まれているはずである.
データにこのような傾向があるかどうかを見るために,データの自己相関を調べる方法がある.自己相関とは,ある時系列データと,そのデータを一定期間だけずらしたデータとの相関のことである.
為替レートの値動きの自己相関が正ならばトレンドの存在を示唆し,逆に自己相関が負なら為替レートは反発しやすいということを意味する.
このページでは最も代表的な通貨ペアであるドル円のヒストリカルデータを用いて,為替レートの自己相関を調べてみる.
ドル円の値動きの自己相関
為替レートの値動きの自己相関を調べる.ある期間の値動きは,
\[ \text{値動き} \, (\text{difference}) = \text{終値} \, (\text{close}) \, – \, \text{始値} \, (\text{open}) \ . \]
と定義する.為替レートの値動きの分布については,為替レートの値動きの従う確率分布を参照のこと.
使用するデータは,ある証券会社の2007年1月から2019年12月までの13年間(計3,371営業日)のヒストリカルデータである.
値動きの日足データの自己相関
ドル円の日足データについて,ある日の値動きとその翌日の値動きの散布図を作成すると,下図のようになる.
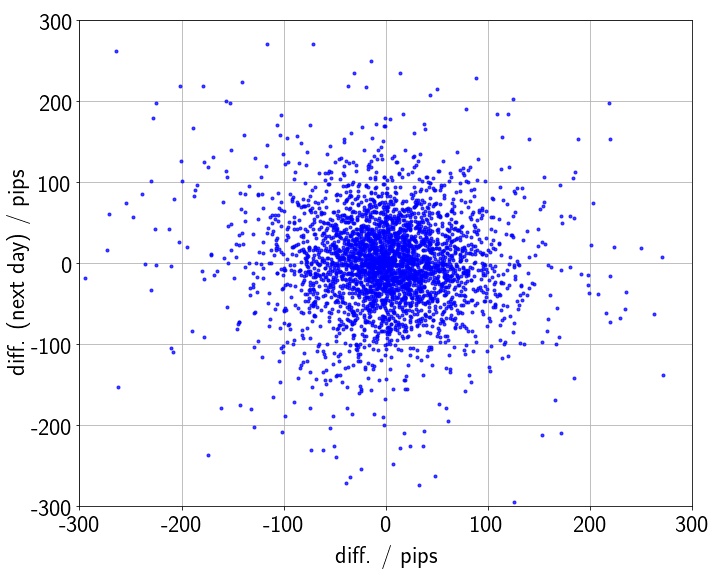
この図を見る限り,ある日の値動きとその翌日の値動きには相関が見られない.相関係数は$-0.055$程度である.
翌日だけではなく,たとえばある日とその一週間後の値動きの相関なども計算できる.そこで,自己相関をとる時間間隔を変えて相関係数を計算してみる.結果は下図のようになる.
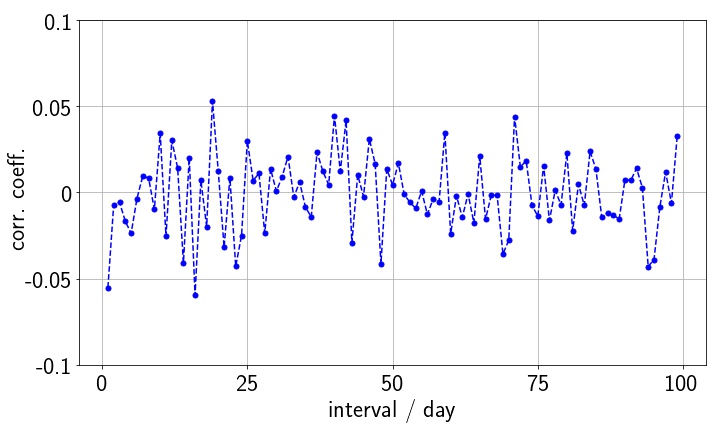
やはりどのような時間間隔を取っても相関係数は小さい.図では時間間隔を100日までしか示していないが,より長期の時間間隔を取っても相関は見られない.
自己相関は時間間隔が長くなるほど小さくなるのが自然なので,図のように時間間隔によらずに相関係数が$-0.05$から$0.05$程度の大きさになっているということは,そもそも自己相関が無いことを示していると言って良い.
値動きデータの自己相関:異なる時間スケールの比較
次に,日足データだけではなく,時間足などの異なる時間スケールのデータの自己相関を調べよう.用いるデータは1時間足から週足までで,以下の通りである.月足や年足はデータ数が少ないので,見かけの相関が出てしまうため排除した.
| データ名 | 1 h | 2 h | 3 h | 4 h | 6 h | 8 h | 12 h | 1 day | 1 week |
|---|---|---|---|---|---|---|---|---|---|
| hours | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 | 6240 |
| データ数 | 80252 | 40353 | 26905 | 20183 | 13459 | 10095 | 6730 | 3371 | 678 |
これらのデータについて,自己相関があるとすれば最も大きいと期待される,単位時間間隔(日足なら1日)だけずらした自己相関を計算する.13年間のデータを1年ごと13個に分けて各年における相関係数を計算すると,以下の図のようになる.
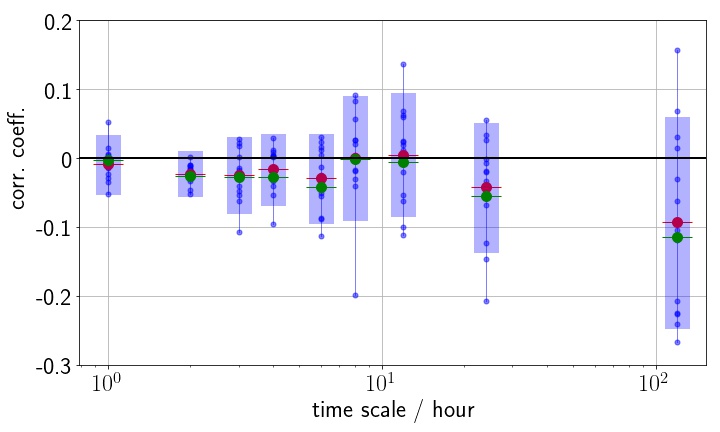
赤い点が各年の相関係数の平均値,青い帯が平均値からの1標準偏差の範囲を表している.緑の点は13年間の全てのデータを使ったときの相関係数である.これを見ると,どの時間スケールでも,相関係数は1標準偏差の範囲で$0$と無矛盾である.時間スケールが大きくなると相関係数(のばらつき)が大きくなっているが,これはデータ数が少なくなることによる統計的なばらつきであると考えられる.
ここまでの解析では,為替レートの値動きのデータから自己相関を見つけることはできなかった.ただし,ここでの解析は大きなサイズのデータを使った粗視的なものであるから,いかなる有意な自己相関も存在しないと主張するものではない.
たとえば,値動きが大部分のランダムウォークと一部のトレンド(相関)から作られている場合,相関が大部分のランダムウォークに覆い隠されて見えなくなることもあり得るだろう.このような可能性を調べるためには,さらなる解析が必要である.
ドル円の値幅の自己相関
ここまでの解析は為替レートの値動きの自己相関について調べてきた.次は値幅について同様の解析を行う.ある期間の値幅は,
\[ \text{値幅} \, (\text{range}) = \text{高値} \, (\text{high}) \, – \, \text{安値} \, (\text{low}) \ . \]
と定義する.為替レートの値幅の分布については,為替レートの値幅の従う確率分布【対数正規分布】を参照のこと.
値幅の日足データの自己相関
2007年から2019年までの13年間のドル円の日足データ(3,371営業日)について,ある日の値幅とその翌日の値幅の相関図は以下のようになる.値幅の対数を取った量は正規分布に従い解析しやすいので,値幅の常用対数を用いて図を作成した.
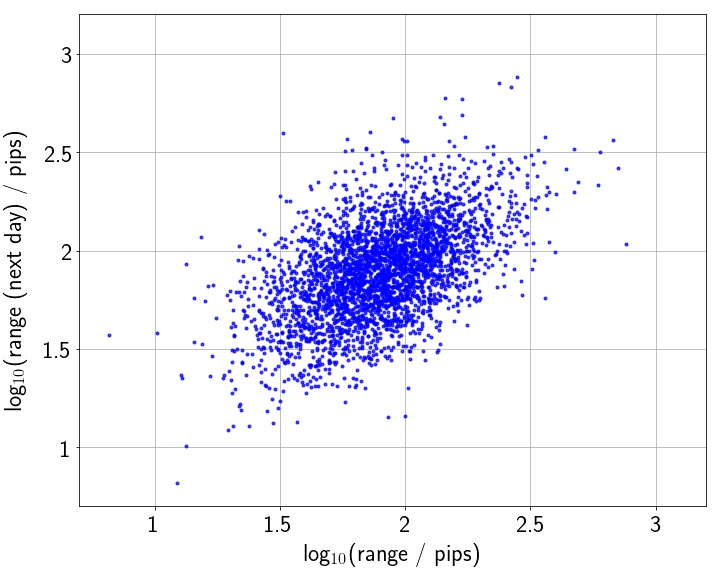
値動きの場合と異なり,ある日の値幅とその翌日の値幅との間に相関があることが,はっきりと見て取れる.相関係数は0.529である.
この結果は,「値幅の大きな(小さな)日の翌日は値幅が大きい(小さい)傾向がある」ということを意味している.日々のボラティリティの大きさには相関があり,相場が落ち着いている期間と荒れている期間が存在するということである.
値動きの場合と同様に,自己相関をとる時間間隔を変えて相関係数を計算してみる.結果は下図のようになる.
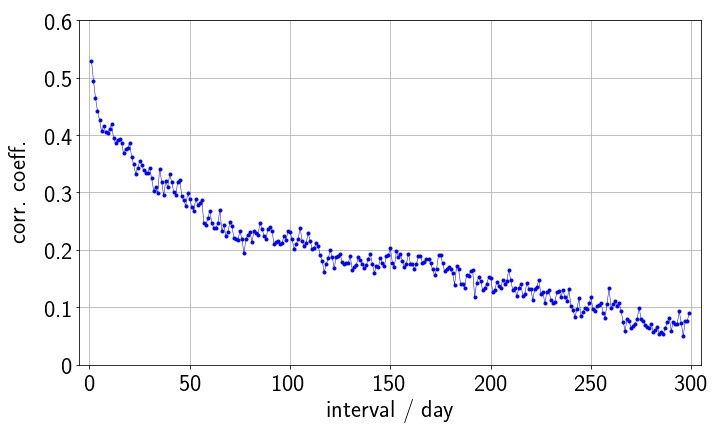
期待されるように,自己相関をとる時間間隔が広くなるほど,相関は小さくなっていくことがわかる.時間間隔が1年(約260営業日)の自己相関は0.1程度で,これくらいになると相関はほぼ無くなる.
値幅データの自己相関:異なる時間スケールの比較
値動きの場合と同様に,各時間スケールの年ごとのデータに対して,単位時間間隔に対する自己相関を計算したものをプロットすると,以下のようになる.
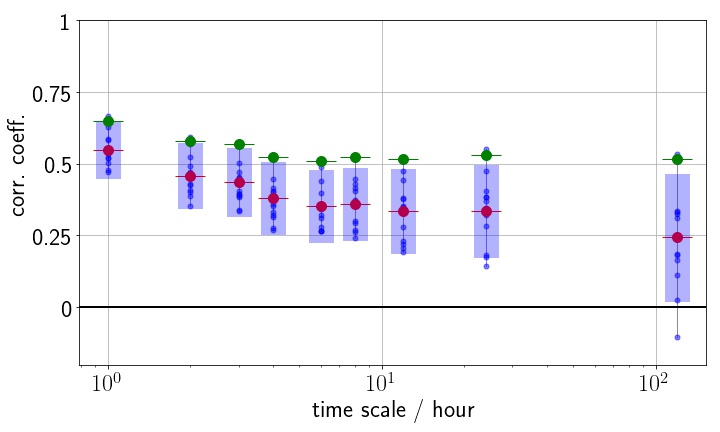
赤い点が各年の相関係数の平均値,青い帯が平均値からの1標準偏差の範囲を表している.緑の点は13年間の全てのデータを使ったときの相関係数である.
どの時間スケールでも為替レートの値幅にはある程度の自己相関があること,自己相関の大きさは時間スケールが大きくなに従いやや小さくなっていくことなどが図から読み取れる.
ここで,全13年間のデータを使ったときの相関係数(緑の点)が,年ごとに計算した相関係数(青い点)よりもはっきりと大きくなっている点についてコメントをしておく.
為替レートの変動が比較的大きな年や小さな年が存在するため,値幅の大きな年のデータが相関図の右上に,値幅の小さな年のデータが左下に集まり,相関図(散布図)が全体として右上がり(左下がり)に伸び,単年で見たときよりも相関が大きくなる.ただし,これは見かけ上の相関ではなく,実際に,年ごとのデータにも(全体と比べると小さいが)有意な相関が見られる.
データを年ごとに分割するというのは,男女混合のデータを男女別に分割したり,全年齢のデータを年齢層ごとに分割したりするのと比べると,ほとんど必然性がない.一見データに相関があるように見えても,男女別や年齢層別のデータを解析する(層別相関を見る)と相関が見られないことがあるというのとは状況が異なる.
値幅の自己相関に基づく値幅予測
先に示したように,ある日の値幅とその翌日の値幅との間には相関係数0.5程度の有意な相関がある.これは,ある日の値幅が大きい(小さい)とその翌日の値幅も大きい(小さい)傾向があることを示している.
値幅は対数正規分布に従うので,ある日の値幅とその翌日の値幅は2変量対数正規分布 [Ref.] に従う.したがって,ある日の値幅が与えられると翌日の値幅の確率分布が得られ,翌日の値幅がどの程度の大きさになるのか予測することができる.値幅の予測はリスクの評価や利幅の設定に応用することができる.
以下に具体的な方法を示す.まず,過去のデータを用いて,対数正規分布のパラメータ$\mu$と$\sigma$を決定する.詳細は為替レートの値幅の従う確率分布【対数正規分布】を参照のこと.さらに,相関図からある日とその翌日の値幅との相関係数$\rho$を計算する.
ある日の値幅$r$(一貫した単位ではかる)が与えられたときに,
\[ \tilde{\mu}(r) = \mu + \rho(\ln(r) – \mu) \ , \quad \tilde{\sigma}^{2} = (1 – \rho^{2})\sigma^{2} \ , \]
と新しいパラメータ$\tilde{\mu}(r)$と$\tilde{\sigma}^{2}$を計算する.$\tilde{\mu}(r)$は値幅$r$に依存するが,$\tilde{\sigma}^{2}$は$r$には依存しない.これらのパラメータが,ある日の値幅が$r$であったときの,その翌日の値幅の条件付き確率分布のパラメータとなる.
こうして得られた新しい分布
\[ f(x; r) = \frac{1}{\sqrt{2\pi\tilde{\sigma}^{2}}x} \exp \left( -\frac{\big( \ln x – \tilde{\mu}(r) \big)^{2}}{2\tilde{\sigma}^{2}} \right) \ , \]
が,ある日の値幅$r$が与えられたときの翌日の値幅の確率分布を与える.
