最終更新日 : 2020/06/05
為替レートの値動き・値幅分布の時間スケール依存性
ある期間の為替レートの値動きと値幅を,それぞれ以下のように定義する.
\begin{align*} \text{値動き} \, (\text{difference}) &= \text{終値} \, (\text{close}) \, – \, \text{始値} \, (\text{open}) \ , \\ \text{値幅} \, (\text{range}) &= \text{高値} \, (\text{high}) \, – \, \text{安値} \, (\text{low}) \ . \end{align*}
他のページで確認したように,値動きは正規分布より尖度の高い分布に従い [Ref],値幅は対数正規分布に従う [Ref].
これを確かめるために用いたのはドル円の日足データであったが,異なる時間スケールや異なる通貨ペアについても同様のことが言える.(ここに図は示さないが,実際に確かめることができる)
このページでは,ドル円の値動き・値幅分布が時間スケールにどのように依存するのかを調べる.通貨ペアどうしの比較は別のページに譲る.
ドル円の値動き・値幅分布の時間依存性
為替レートの変動の大きさを特徴付ける量としては,たとえば値動きの標準偏差や値幅の最頻値・中央値・平均値が挙げられる.これらの量を順にdiff_std,range_mode,range_median,range_meanと呼ぶことにしよう.
ドル円の為替レートのデータは,ある証券会社の2007年1月から2019年12月までの13年間(計3,371営業日)のヒストリカルデータを用いる.
用いたデータの時間スケールとデータ数は以下の通りである.
| データ名 | 1 h | 2 h | 3 h | 4 h | 6 h | 8 h | 12 h | 1 day | 1 week | 1 month | 1 year |
|---|---|---|---|---|---|---|---|---|---|---|---|
| hours | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 | 120 | 528 | 6240 |
| データ数 | 80252 | 40353 | 26905 | 20183 | 13459 | 10095 | 6730 | 3371 | 678 | 156 | 13 |
時間足としては24時間の約数を選んだ.また,土日を除いた営業日数を考慮し,週足は5日,月足は22日,年足は260日として,時間に換算した.
これらのデータに対して,上で挙げた4つの統計量を時間に対してプロットすると,以下の図を得る.ここで,値幅の中央値$m$と平均値$\mu$はデータから直接計算した量であるが,最頻値$M$は,値幅分布が対数正規分布に従うことを用いて,
\[ M = \frac{m^{3}}{\mu^{2}} \ , \]
を使って中央値と平均値から計算した.最頻値と中央値,平均値の間の関係については,対数正規分布について知っておくべきことを参照のこと.
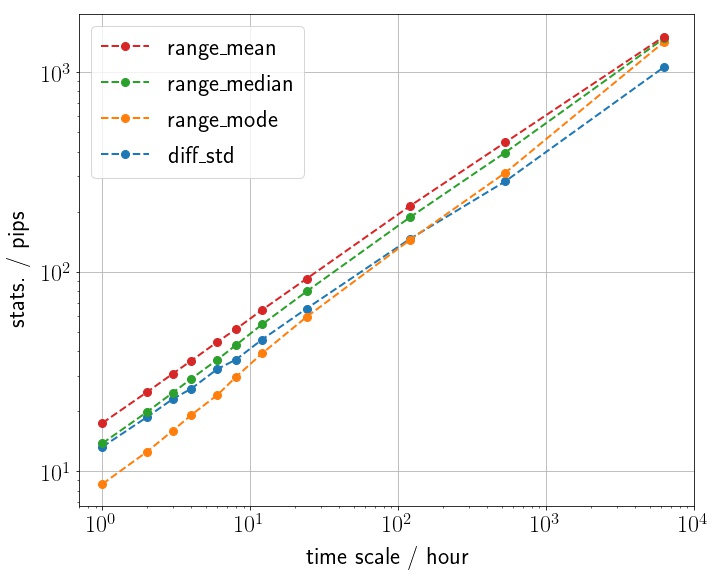
図を見ると,どのデータも同じ傾きを持つ直線上にきれいに並んでいることが分かる.両対数目盛で直線に並ぶということは,各統計量が時間の冪乗に比例することを表している.その傾きは両対数目盛でだいたい1/2程度であることが読み取れる.つまり,横軸が2桁変わると縦軸が1桁変わる.
この関係を定量的に確かめてみよう.両軸の対数を取ったものを最小二乗法を用いて直線$y = ax + b$で線形フィットすると,パラメータ$(a, b)$は以下のように求まる.
| diff_std | range_mode | range_median | range_mean | |
|---|---|---|---|---|
| $a$ | 0.4985 | 0.5826 | 0.5121 | 0.5356 |
| $b$ | 2.5790 | 2.1600 | 2.8761 | 2.6374 |
値動きの最頻値(range_mode)は0.58とやや大きいものの,確かにどのデータでも傾き$a$は約$1 / 2 = 0.5$であることが分かる.(フィッティングの誤差をきちんと評価すれば,range_modeも他の統計量の振舞いからそれほど大きくずれているわけではないと期待される)
この振舞いをさらによく見るには,先ほどの図の縦軸に時間スケールの平方根をかけてみればよい.結果は下の図のようになる.
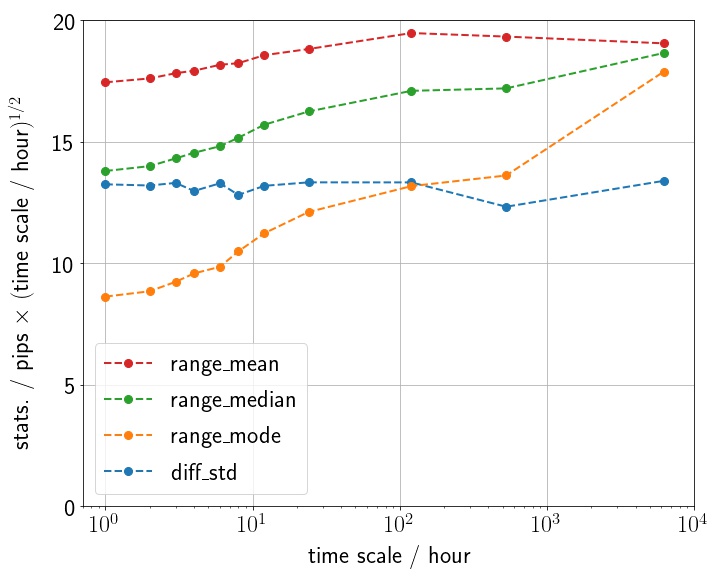
こちらも,値動きの最頻値(range_mode)はやや振舞いが異なるが,全体としてグラフが平らになっていることが分かる.これらのことから,値動き・値幅分布の種々の統計量(まとめて「変動の大きさ」と呼ぶことにする)は時間スケールの平方根に比例することが分かる.
\[ \text{変動の大きさ} \propto \sqrt{\text{時間スケール}} \ . \]
これは非常に重要な結果である.為替レートがどの程度の時間スケールで典型的にどの程度変動し得るのかというのは,取引手法を構築する際に最も重要な情報のひとつである.
また,為替レートの変動の大きさが時間スケールの平方根に比例するという事実は,為替レートの変動がランダムウォークであることを示唆している.もちろんこれは必要条件であって十分条件ではないのだが.
