為替レートの値幅の従う確率分布【対数正規分布】

為替レートの値幅の定義

ある一定期間の為替レートの変動を考えたとき，その期間における「高値と安値の差」を値幅と呼ぶことにしよう．（これに対して，終値と始値の差を，このサイトでは値動きと呼んでいる）

\[ \text{値幅} \, (\text{range}) = \text{高値} \, (\text{high}) \, – \, \text{安値} \, (\text{low}) \ . \]

為替レートは2つの通貨の価値の「比」なので，値幅は「差」ではなく「比」で定義する方が適切かもしれない．しかしながら，為替レートに対してその変動幅が小さい場合には，両者に違いはない．

たとえばドル円の場合，為替レートが1ドル＝100円（$r = 100 \, \text{jpy} / \text{usd}$）程度のオーダーであるのに対して，一日の変動幅は高々$\Delta r = 100 \, \text{pips} = 1 \, \text{jpy} / \text{usd}$であるので，差と比を使ったときの誤差は高々$1\%$程度である．

より長い期間を考える場合や変動率の大きな通貨ペアを考える場合には，この違いは無視できないほど大きくなるかもしれない．その場合には，より数学的に扱いやすい方（より単純な確率分布に従う方）を値幅の定義とすればよい．

為替レートの値幅の従う確率分布【対数正規分布】

為替レートの値幅の分布（確率分布）は，かなり良い精度で「対数正規分布」で表される．対数正規分布とは，

\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}x} \exp \left( -\frac{(\ln x – \mu)^{2}}{2\sigma^{2}} \right) \ , \]

という形の分布で，$\mu$と$\sigma^{2}$はこの分布を特徴付けるパラメータである．パラメータ$\mu$と$\sigma^{2}$は，それぞれ対応する正規分布の平均値と分散であり，対数正規分布の平均値や分散ではないことに注意しよう．対数正規分布について知っておくべき性質については，対数正規分布について知っておくべきことにまとめてある．

このページでは，為替レートの値幅分布が実際に対数正規分布に従っていることを，ドル円の日足データを例として確かめてみる．異なる期間や異なる通貨ペアについての解析は，別のページに譲ることにする．

ドル円の日足データの値幅分布

ドル円の日足データには，ある証券会社の2007年1月から2019年12月までの13年間（計3,371営業日）のヒストリカルデータを用いた．これらのデータから値幅のヒストグラムを作ると，下図のようになる．

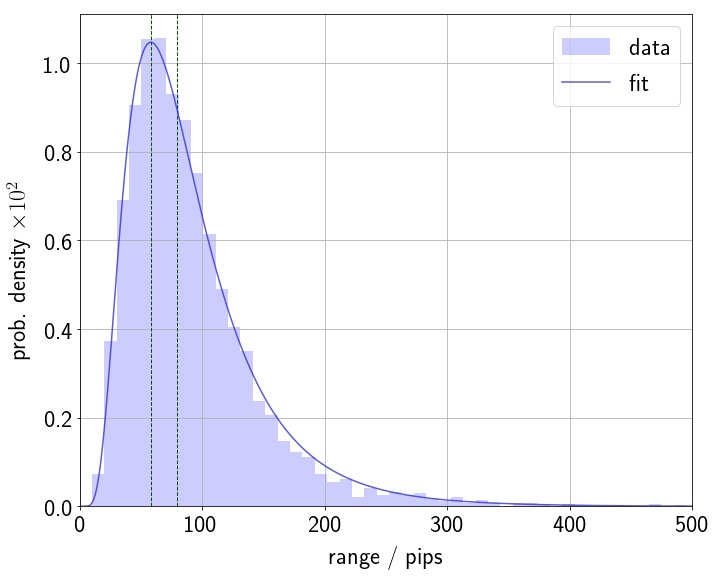
横軸は$\text{pips} = 0.01 \, \text{jpy} / \text{usd}$を単位とした値幅，縦軸は正規化した度数（確率密度）である．また，データに最も良くフィットする対数正規分布を図に重ねて示した．この図を見ると，確かに値幅分布が対数正規分布に従っていると言えそうである．

図中の対数正規分布のパラメータは$\mu = 4.377, \, \sigma^{2} = 0.3135$である．これらは，値幅の対数をとったデータ（このデータは正規分布に従う）の中央値と（不偏）分散から得られた値である．平均値は少数の大きな値を持つデータに依存しやすいため，$\mu$を求めるのに平均値の代わりに中央値を用いた．正規分布では，中央値と平均値は等しい．

為替レートの値幅分布が対数正規分布に従うというこの事実は，為替レートの変動がランダムウォーク的であることを強く示唆している．（もちろん，あくまでも必要条件であって十分条件ではないのであるが）

値幅分布のランキングプロット

対数正規分布によるフィット がどの程度うまくいっているのかを確かめるには，ランキングプロットを見てみるとよい．

ランキングプロットとは，横軸にデータの値（つまり値幅），縦軸にその値の全データ中の順位を示したものである．上で用いたのと同じドル円の日足データに対してランキングプロットを作成すると，下図のようになる．図を見やすくするために両対数プロットにしてある．

図には対数正規分布によるフィット （青の波線）も示した．この線$\text{rank}(x)$は，対数正規分布の累積分布関数を$F(x)$と書けば，

\[ \text{rank}(x) = N[1 – F(x)] \ , \]

と表すことができる．$N$はデータ数（今の場合$N = 3371$）である．

図を見ると，値幅が小さいところ（$\sim 300 \, \text{pips}$）では対数正規分布によるフィットがうまくいっているが，値幅が大きいところではズレが大きくなっていることが分かる．

このように，大部分のデータはある特定の分布に従うが，分布の裾野のあたりでは分布からのズレが大きくなるというのは，様々なデータに対してよく見られる現象だそうである．今回の場合には，裾野の部分にもう一つ対数正規分布を重ねることで，全体をうまくフィットできそうである（二重対数正規分布）．

裾野の振舞いから為替レートの大変動時の情報が得られるので非常に重要ではあるが，このページにあまり詰め込むのもどうかと思うので，この精査は別のページに譲ることにしよう．