最終更新日 : 2020/04/19
対数正規分布について知っておくべきこと
対数正規分布の確率密度関数は,
\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}x} \exp \left( -\frac{(\ln x – \mu)^{2}}{2\sigma^{2}} \right) \ , \]
で定義される.変数$x$は正の値をとる.また,$\mu$と$\sigma^{2}$は分布を特徴付けるパラメータである.
いくつかのパラメータの組に対して対数正規分布の関数形をプロットすると,下図のようになる.
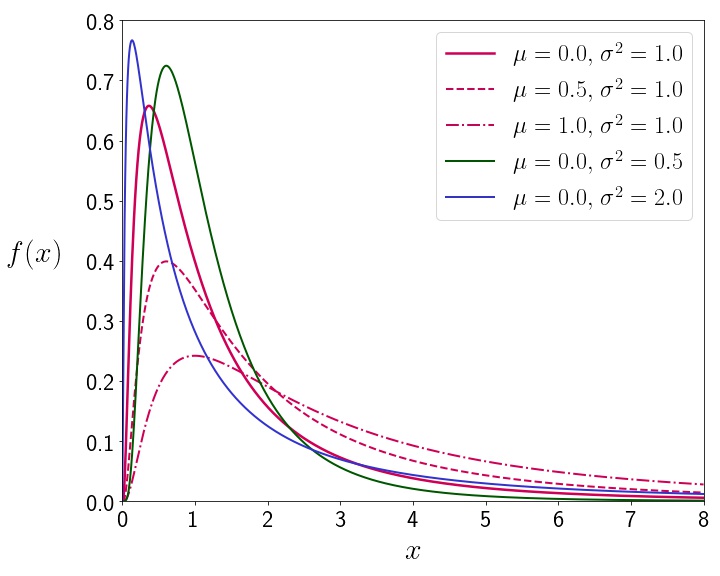
対数正規分布と正規分布の関係
「ある確率変数が対数正規分布に従う」とは「確率変数の対数をとったものが正規分布に従う」ということである.実際,新しい変数を$y = \ln x$で定義し,$f(x)dx = g(y)dy$と変数変換を行うと,$y$についての確率密度関数は,
\[ g(y) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp \left( -\frac{(y – \mu)^{2}}{2\sigma^{2}} \right) \ , \]
のように,平均$\mu$,分散$\sigma^{2}$の正規分布となる.ここで,確率密度の変換なので,$dx$や$dy$という微小幅をかけて変換しなければならないことに注意しよう.
対数正規分布を特徴付けるパラメータ$\mu$と$\sigma^{2}$は,対応する正規分布の平均値と分散に対応し,対数正規分布そのものの平均値や分散ではないことに注意が必要である.
対数正規分布の累積分布関数
$x$が$x_{0}$以下の値をとる確率$F(x_{0})$は,確率密度関数を$0$から$x_{0}$まで積分して,
\[ F(x_{0}) = \int_{0}^{x_{0}}dx \, f(x) \ , \]
と計算できる.この関数$F(x)$を累積分布関数と呼ぶ.累積分布関数は下図のようになる.
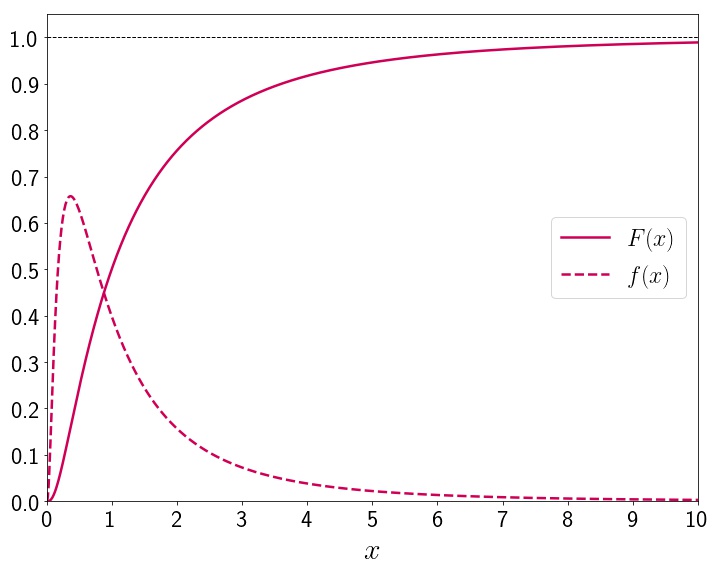
対数正規分布の場合,この関数を初等関数で書くことはできないが,数値的に任意の精度で計算することができる.
ここで,誤差関数(error function)$E(x)$を
\[ E(x) = \frac{1}{\sqrt{2\pi}} \int_{-x}^{x}dt \, e^{-t^{2} / 2} = \frac{2}{\sqrt{2\pi}} \int_{0}^{x}dt \, e^{-t^{2} / 2} \ , \]
で導入すると,累積分布関数$F(x)$は
\[ F(x) = \frac{1}{2} \left[ 1 + E \left( \frac{\ln x – \mu}{\sigma} \right) \right] \ , \]
と書くことができる.
ちなみに,誤差関数は
\[ {\text{erf}}(x) = \frac{2}{\sqrt{\pi}} \int_{0}^{x} dt \, e^{-t^{2}} \ , \]
で定義されることが多い.${\text{erf}}(x) = E(\sqrt{2}x)$の関係があり,${\text{erf}}(x)$を使うと,累積分布関数$F(x)$は
\[ F(x) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{\ln x – \mu}{\sqrt{2}\sigma} \right) \right] \ , \]
と書くことができる.
誤差関数は${\text{erf}}(x)$よりも,先に定義した$E(x)$の方が便利なことが多い.例えば,
\[ \begin{align} E(1) &= 0.6826\dots \ , \\ E(2) &= 0.9544\dots \ , \\ E(3) &= 0.9973\dots \ , \end{align} \]
のように,いわゆる「$n$-シグマ」の値が,$E(n)$とシンプルに表される.${\text{erf}}(x)$を使うと,$n$-シグマの値は${\text{erf}}(n / \sqrt{2})$と書かなくてはならない.
対数正規分布の平均値・分散・最頻値・中央値
対数正規分布の種々の統計量を,パラメータ$\mu$と$\sigma^{2}$で表しておこう.平均値$\mu_{x} = \braket{x}$は,
\[ \mu_{x} = \braket{x} = \int_{0}^{\infty} dx \, xf(x) = \int_{-\infty}^{\infty} dy \, e^{y} g(y) = e^{\mu + \sigma^{2} / 2} \ , \]
と計算できる.対応する正規分布に変数変換してから計算すると良い.
同様に,$x^{2}$の平均値$\braket{x^{2}}$は,
\[ \braket{x^{2}} = \int_{0}^{\infty} dx \, x^{2}f(x) = \int_{-\infty}^{\infty} dy \, e^{2y} g(y) = e^{2\mu + 2\sigma^{2}} \ , \]
と計算できるので,分散$\sigma_{x}^{2}$は
\[ \sigma_{x}^{2} = \braket{x^{2}} – \braket{x}^{2} = e^{2\mu + \sigma^{2}}(e^{\sigma^{2}} – 1) \ , \]
と求まる.
正規分布と異なり,対数正規分布は右側に長い裾を持つ非対称な分布なので,最頻値や中央値は自明ではない.これらを計算しよう.最頻値は分布のピークなので,分布関数の極値を求めれば良い.
\[ f'(x) = \frac{f(x)}{x} \left[ 1 + \frac{\ln x – \mu}{\sigma^{2}} \right] \ , \]
であるから,$f'(M_{x}) = 0$を解いて,最頻値は$M_{x} = e^{\mu – \sigma^{2}}$と求まる.
中央値$m_{x}$は,累積分布関数$F(x)$を使って$F(m_{x}) = 1 / 2$と定義される.ここで,
\[ F(m_{x}) = \int_{0}^{m_{x}} dx \, f(x) = \int_{-\infty}^{\ln m_{x}} dy \, g(y) \ , \]
であるから,$F(m_{x}) = 1 / 2$となるのは$\ln m_{x} = \mu$のときである.すなわち,中央値は$m_{x} = e^{\mu}$と求まる.
| 最頻値 | $M_{x} = e^{\mu – \sigma^{2}}$ | $F(M_{x}) = \dfrac{1}{2} \left[ 1 + E(-\sigma) \right]$ |
| 中央値 | $m_{x} = e^{\mu}$ | $F(m_{x}) = \dfrac{1}{2}$ |
| 平均値 | $\mu_{x} = e^{\mu + \sigma^{2} / 2}$ | $F(\mu_{x}) = \dfrac{1}{2} \left[ 1 + E(\sigma / 2) \right]$ |
| 分散 | $\sigma_{x}^{2} = e^{2\mu + \sigma^{2}}(e^{\sigma^{2}} – 1)$ |
なお,重要な統計量はWikipediaのページにまとまっているので,適宜参照するとよい.
